Problem
A large retail lawn care dealer currently provides a two-year warranty on all lawn mowers sold at its stores. A new employee suggested that the dealer could save money by just not offering the warranty. To evaluate this suggestion, the dealer randomly decides whether or not to offer the warranty to the next 500 customers who enter the store and express an interest in purchasing a lawn mower. Out of the 250 customers offered the warranty, 91 purchased a mower, as compared to 53 of 250 not offered the warranty.
a. Place a 95% confidence interval on the difference 
in the proportion of customers purchasing lawn mowers with and without the warranty.
b. Test the research hypothesis that offering the warranty will increase the proportion of customers who will purchase a mower. Use α = .01 .
c. Based on your results from parts (a) and (b) should the dealer offer the warranty?
Step-by-step solution
Step 1 of 10
A dealer of land mowers wants to know whether offering the warranty is really helpful in good sales. Out of next 500 customers who entered the store and expressed an interest in purchasing a land mower, 250 customers were offered warranty and 250 were not offered any warranty.
Out of 250 customers who were offered warranty, 91 purchased the mower. And out of 250 customers who were not offered warranty, 53 purchased the mower.
Comment Step 2 of 10
If we take these two groups of customers as two different random samples, we have:
For the random sample of customers who were offered warranty
Sample size,
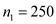
Proportion of customers who purchased the mower when offered warranty,
For the random sample of customers who were not offered warranty
Sample size,
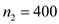
Proportion of customers who purchased the mower when not offered warranty,
Comment Step 3 of 10
a) We want to place a 95% confidence interval on the difference in the proportion of the customers purchasing lawn mowers with or without warranty. In other words, we want to construct 95% confidence interval for
. The confidence interval is given by:
Since, we want to compute 95% confidence interval,
Use Standard Normal table to get,
Comment Step 4 of 10
Here,
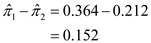
Comment Step 5 of 10
The 95% confidence interval is:
The 95% confidence interval for the difference in the proportion of the customers purchasing lawn mowers with or without warranty is
.Comment Step 6 of 10
b) We want to test the hypothesis that offering the warranty will increase the proportion of customers who will purchase a mower.
The hypotheses are:
or 
warranty will not increase the proportion of customers who will purchase a mower.
or
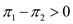, warranty will increase the proportion of customers who will purchase a mower.The test statistic is:
Comment Step 7 of 10
Here,
Also,
Hence, large sample approximation to z is valid here.
Comment Step 8 of 10
We have already computed that
.
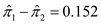Comment Step 9 of 10
This gives,
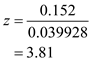
Using Standard Normal table (z-table),
Rejection region is given as: Reject
if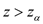 
We can see that
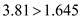or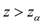
, so there is sufficient evidence to reject 
at level of significance 0.05. Hence, we conclude that at level of significance 0.05, there is significant evidence that warranty will increase the proportion of customers who will purchase a mower.Comments (1) Step 10 of 10
c) The 95% confidence interval for the difference in the proportion of the customers purchasing lawn mowers with or without warranty is
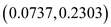. Here, the confidence interval does not contain zero which means that the difference in the proportion is always greater than zero, that is, 
is greater than zero or 
. So, the proportion of customers who purchase the mower when warranty is given by the dealer is more than the proportion of customers who purchase the mower when warranty is not given by the dealer.Also we are accepting the hypothesis that warranty will increase the proportion of customers who will purchase a mower.
On the basis of this result, we can say that dealer should offer the warranty.
Comment
