13. The 60° strain rosette is mounted on a beam. The following readings are obtained for each gauge: ?.-200 (10-6 ) , ?,--450(10 6 ) , and ?,-250 (106 ) . Determine the in-plane principal strains. 30° 30 60°
Expert Answer
Comment
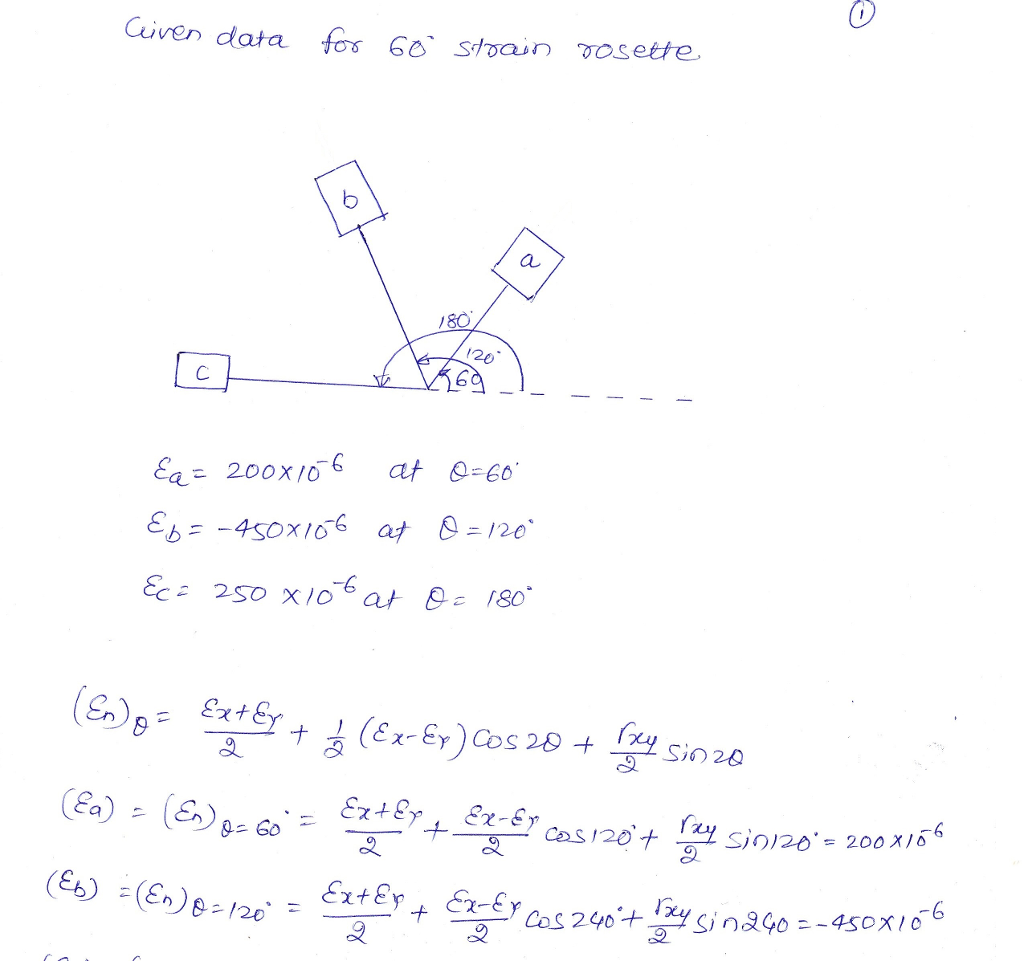
![(Esr.fr)± J(Arg.) +仙] 450 .933 χ 158 plae max 901.869 x6Crs principal shouĄD ε,-450,9 33x106 (An) plane](https://d2vlcm61l7u1fs.cloudfront.net/media%2Fc1c%2Fc1c32e10-87a8-4033-9664-2ddf0d42952f%2FphpjTVr3p.png)
Civen data 80 6 6 S20 120P ã…¡ О.SG + О 86c R = 200xt δ6 ナã†Rs 375, 288x166 P- O-CO -O-846 RP -450x106 (ツ 250x10 å‰ o2(Esr.fr)± J(Arg.) +ä»™] 450 .933 χ 158 plae max 901.869 x6Crs principal shouÄ„D ε,-450,9 33x106 (An) plane
Please show all steps to get these answers
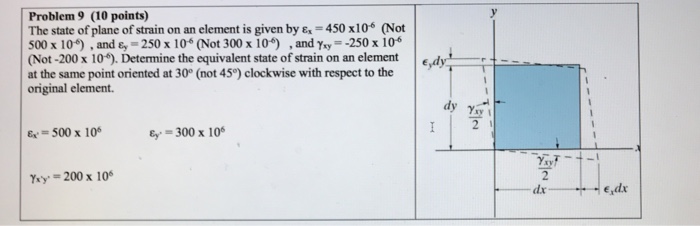
Problem 9 (10 points) The state of plane of strain on an element is given by ?.-450 x 106 (Not 500 x 10*) , and ?' 250 x 106 (Not 300 x 10") , and Yr,--250 x 10-6 (Not -200 x 10*). Determine the equivalent state of strain on an element at the same point oriented at 30° (not 45°) clockwise with respect to the original element. dy = 500 x 106 ?=300 x 106 200x 10 2 dx e,dx
Expert Answer
Comment
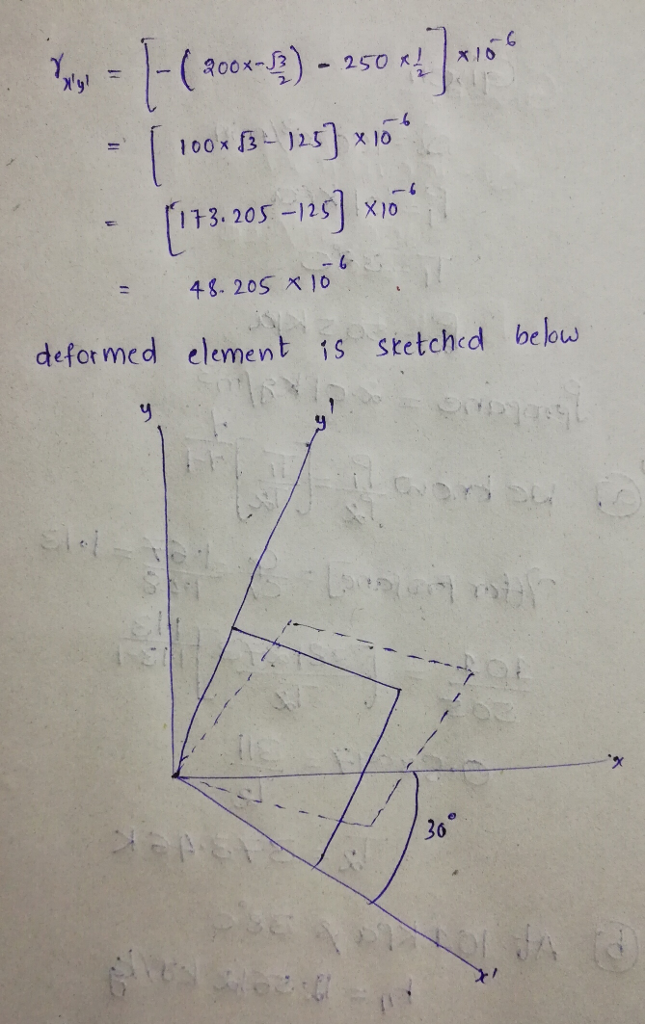Given thot the x- component of the state of stron at the Y- component of the statc of stroun at the point is ()- 450x 10 the point is (fy)-250 。 the shar stran ()20X1o 1 compovent er tn onented anglk )0 ri) we know that normal strain in ' direction 100 x10 1200 x10 CoS60 12s x1otsino) Normal stroin in y ditcction 2. 020 cosso las sinco 166 1.300-62-5x1-734] (G18 Now shear strain wr-(6-5s:m)2) ri73, 205-1251 X)。 48. 20S x 10 deformed element 1S Stetched be ow ズ 36
Problem 5) The state of strain at a point on a wrench has components Ex= 120(10), Ey=-180(10“), Yxy = 150(10) Use the strain-transformation equations to determine (a) the in-plane principal strains and (b) the maximum in-plane shear strain and average normal strain. In each case specify the orientation of the element and show how the strains deform the element within x - y plane. Problem 6) Solve Prob. 5 using Mohr's circle.
Expert Answer
- Comment
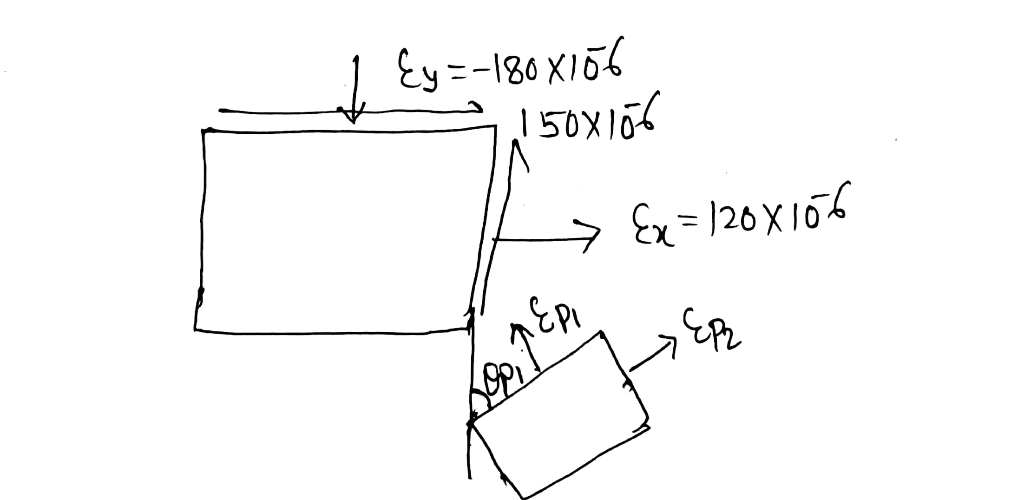As per chegg policy 1st question is done please ask again rest of the questionComment for any doubt about this solution thank youDon't forget to upvote if you got your answerV Problem 5 Giren Ex= 120X106 , &y=-180x166 , Yay= 150X106 - strain transformation equation, Principal Strains Epi o e by + SCEx£y)2 + Nagy | SP :P = (120-180 x + 12 -18ok 3-4 (75x15 ) = -30x 106 + 169170 X166 Inplane Principal pe strain Epi= 137178106 1 Ep2 = -197178156 - manimum in plane shear strain = {pi-EP2 1 = [[3717-(-1977)] X166 = 335.4X106 average normal strain - Epit {P2 -16717X164 197.78 = -15X166 ? orientation of Principal strain tan 20p, = 21 20 = 2 (Yuy/2). 150X106 - 1 20P1 = tan' $ = 26156 Opi = 13.280 , 0P2= 90+13.28 tom 202, - - Eutty = (-120-180)x1= 750x1067 202,7 -631430 Oq= -31.710 Oz= 90-311710 dy 120+1807X706 3 = 103:28 O Quey -5812901 2y =-l84 X164 - 156x164 | 7 x 26x164
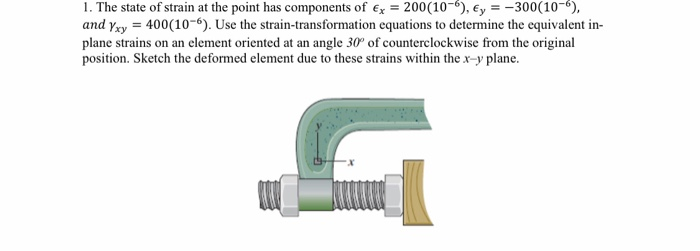
1. The state of strain at the point has components of Ex = 200(10-), ey = -300(10-), and you = 400(10-6). Use the strain-transformation equations to determine the equivalent in- plane strains on an element oriented at an angle 30 of counterclockwise from the original position. Sketch the deformed element due to these strains within the x-y plane.
Expert Answer
- Comment
Given data for case Ex- 200 x156 Trey = 4oxio Note & The following sign convenstion we use: tue normal strain indicate elongation and Eve) normal strain indicate compression per unit length. Shear strain is Positive when angle decreased and are when angle increase. Representation of above case & -- - - - - Tusha ken so value of Sirain at auglle Q = 301 (cow) Et sa te te for any cosao + Hay sinzo En e 200 +1,30) x io + 260-1-30) xcom cos (2830) 2 Tee 245.205 kröf" am + Leo xed sin ci and also Ex + ay = Ext by 248.205 yvób + dy = 26x10* + (-360) x 105 E' = -345.205 xvõt]Yvelyn - Cen- cog) sin2o + Yry cos 20 Yalyl ar (200+300)x100 589 600 + 4coxioo costo & Jazly! -233.01 X166 Auswir respresentation on element Ty, transformed slale.
120 MPa 13. Determine the principal stress, the maximum inplane shear stress, and average normal stress. Specify the orientation of the element in each case. 300 MPa
Expert Answer
- Comment
Given "Рух 1 2 [Pa ny = 300 mpa for principal stresses Tatty (ox gj + Tuy 2 2. Ð (кар, үер, then, T + Tay 1, 2 - tr3 T = 4oompa = -3 cm f1a . strans are . The principal Е Зm mp4 1, 2-3 мра Maximum Shear stres, | 0 - Uy Tmel? (7sy ) 2 Twен Ñ 1. О SHOT ON REDMI 7 AI DUAL CAMERA emix - Зоо үчү а.230 Tith Average Normal stress, Targ < 3004300) 2 = 300-300 2 Cyn 2/compa Cay=300mla Sea-Boompa =3iompa may shear stres, iman 23.00 MPa SHOT ON REDMI 7 AI DUAL CAMERA
Assignment Determine the equivalent state of stress if an element is oriented 25° counterclockwise from the element shown by using Mohr's circle. 550 MPa
Expert Answer
- Comment
* Given the element have shear stresses y-face ssompa a-face Teu = -550 mpa normal stresses - Ssompa Oq=0 Oy =0 To Construct mohr's circle -> Draw the coordinate axes with transformed - stress variables say Osco & Tay the center of cirle c= Caug a on to » Rading of circle can be determined from stress points. A,B stresses on any faces A(0, -550 mpa) Blo, t550 mpa)to Coy, Try) Moht's circle of the given slvess conditions: Gogi K O CO, Cary) -259) D(-421-32,-35305) E1423.32, +380-5) TALOx, Txy) - Draw the circle joining A&B as diametrical points { cas centre which is the circle (motris) ~ To find the transformed coordinates, measure 20 = 2x25° - 50° anticlock wise from CA & CB A is corresponding to oro Dis to 0250 - the coordinates of D&E are the stresses on 1. transformed plane. - They can be cross checke with - x = x tomt 2 (68204 Tay sina - - 550x sin soo = -421.32 mpa Txo, a - Ty G20 =-(-353.s) = 353.5 mpa. ay = 421.32 mpa.
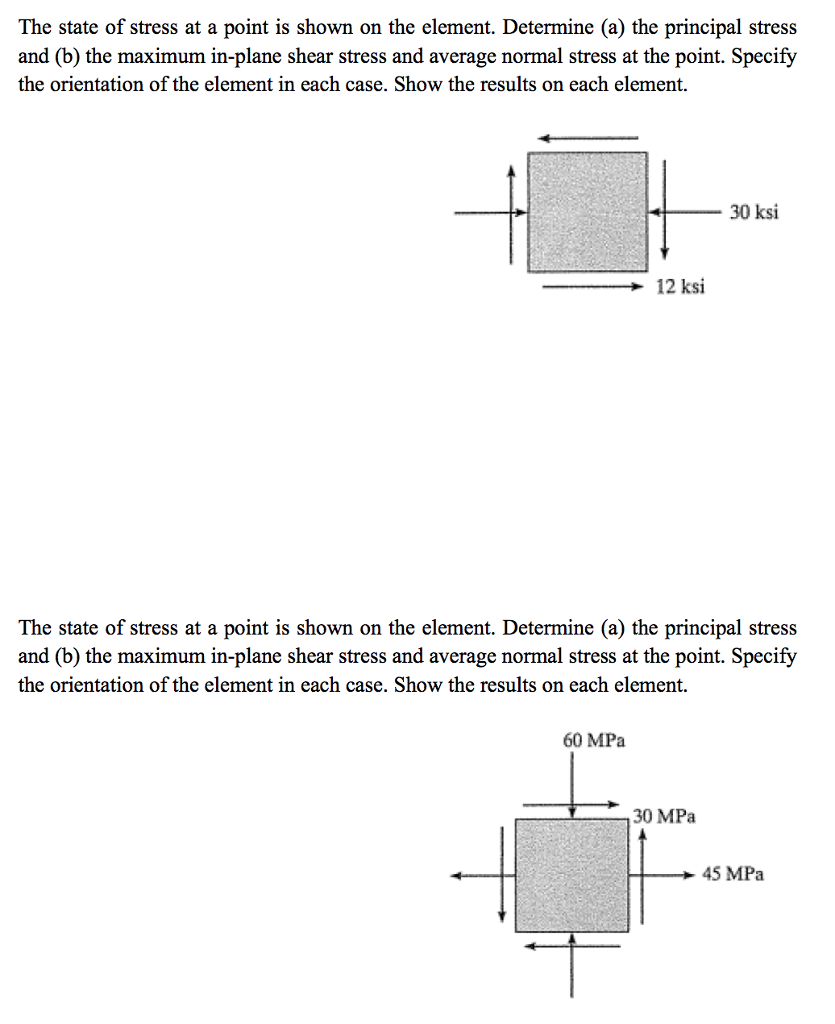
The state of stress at a point is shown on the element. Determine (a) the principal stress and (b) the maximum in-plane shear stress and average normal stress at the point. Specify the orientation of the element in each case. Show the results on each element. 30 ksi 12 ksi The state of stress at a point is shown on the element. Determine (a) the principal stress and (b) the maximum in-plane shear stress and average normal stress at the point. Specify the orientation of the element in each case. Show the results on each element. 60 MPa 30 MPa 45 MPa
Expert Answer
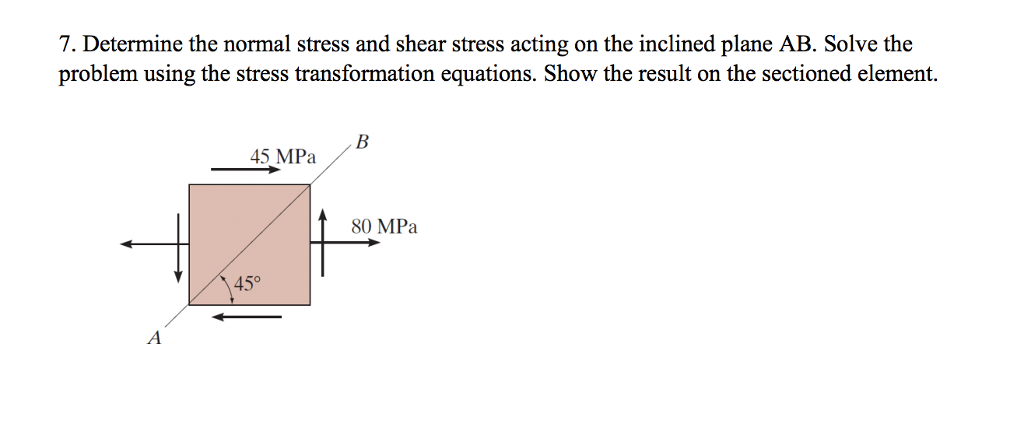
7. Determine the normal stress and shear stress acting on the inclined plane AB. Solve the problem using the stress transformation equations. Show the result on the sectioned element. 45 MPa 80 MPa 450
Expert Answer
- Comment
![LIS HPa 80+0]+1 [80-0] Cos 2(45) = Bo MPa 45 45sin 2(45) 一 0-45-5 P Snf -uo hPa (*)o Compress,on . uohpa =](https://d2vlcm61l7u1fs.cloudfront.net/media%2F900%2F900017ed-06cb-440a-babd-a29300a9bd99%2FphpNJe718.png)
LIS HPa 80+0]+1 [80-0] Cos 2(45) = Bo MPa 45 45sin 2(45) 一 0-45-5 P Snf -uo hPa (*)o Compress,on . uohpa =
Prove that the sum of the normal stresses (in plane stress) is constant for any rotation of the coordinate system (i.e. show that ?x+?y=?x?+?y? f or any ? in the figure below).
Prove that the sum of the normal stresses (in plane stress) is constant for any rotation of the coordinate system (i.e. show that ?x+?y=?x?+?y? f or any ? in the figure below).
Expert Answer
- Commentσx' = (σx+σy)/2+(σx-σy)/2 cos(2θ)+τxysin(2θ)σy' = (σx+σy)/2-(σx-σy)/2 cos(2θ)-τxysin(2θ)Therefore,σx' + σy' = (σx+σy)/2+(σx-σy)/2 cos(2θ)+τxysin(2θ)+ (σx+σy)/2-(σx-σy)/2 cos(2θ)-τxysin(2θ)= σx+σy
ليست هناك تعليقات:
إرسال تعليق