Problem
Consider a 5-m-high, 8-m-long, and 0.22-m-thick wall whose representative cross section is as given in the figure. The thermal conductivities of various materials used, in W/m·K, are kA = kF =2,kB =8, kc = 20, kD = 15, and kE =35. The left and right surfaces of the wall are maintained at uniform temperatures of 300°C and 100°C, respectively. Assuming heat transfer through the wall to be one-dimensional, determine (a) the rate of heat transfer through the wall; (b) the temperature at the point where the sections B, D, and E meet; and (c) the temperature drop across the section F. Disregard any contact resistances at the interfaces.
Step-by-step solution
Step 1 of 13
a)Draw the cross section of thick plane wall shown as follows:
thick plane wall shown as follows: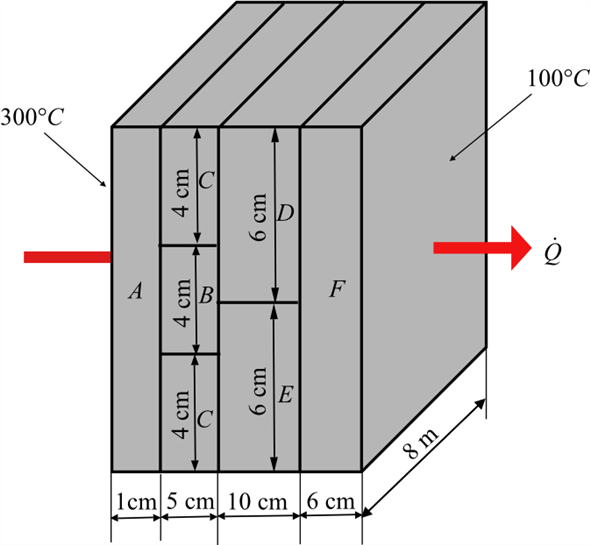
Comment Step 2 of 13
Draw the thermal resistance network due to conduction as shown below.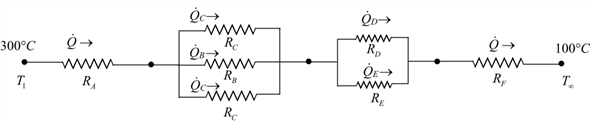
Comment Step 3 of 13
Calculate the thermal resistance in wall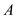 due to conduction, by using the equation as shown below.
due to conduction, by using the equation as shown below.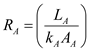 Here, the thickness of the wall
Here, the thickness of the wall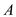 is
is 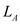 , thermal conductivity of wall
, thermal conductivity of wall 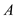 is
is 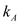 and the area normal to the direction of heat flow through
and the area normal to the direction of heat flow through 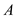 is
is 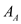 .Substitute
.Substitute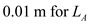 ,
,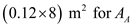 and
and 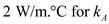 .
.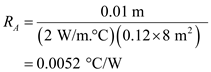
Comments (8) Step 4 of 13
Calculate the thermal resistance in wall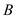 due to conduction, by using the equation as shown below.
due to conduction, by using the equation as shown below.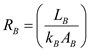 Here, the thickness of the wall
Here, the thickness of the wall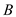 is
is 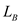 , thermal conductivity of wall
, thermal conductivity of wall 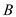 is
is 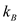 and the area normal to the direction of heat flow through
and the area normal to the direction of heat flow through 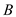 is
is 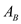 .Substitute
.Substitute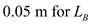 ,
,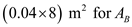 and
and 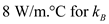 .
.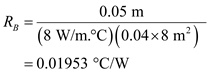
Comment Step 5 of 13
Calculate the thermal resistance in wall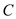 due to conduction, by using the equation as shown below.
due to conduction, by using the equation as shown below.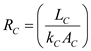 Here, the thickness of the wall
Here, the thickness of the wall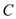 is
is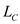 , thermal conductivity of wall
, thermal conductivity of wall 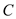 is
is 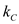 and the area normal to the direction of heat flow through
and the area normal to the direction of heat flow through 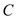 is
is 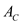 .Substitute
.Substitute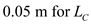 ,
, 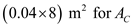 and
and 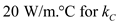 .
.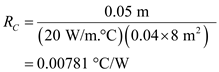
Comment Step 6 of 13
Calculate the thermal resistance in wall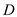 due to conduction, by using the equation as follows:
due to conduction, by using the equation as follows: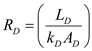 Here, the thickness of the wall
Here, the thickness of the wall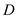 is
is 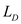 , thermal conductivity of wall
, thermal conductivity of wall 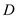 is
is 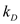 and the area normal to the direction of heat flow through
and the area normal to the direction of heat flow through 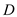 is
is 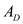 .Substitute
.Substitute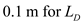 ,
,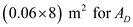 and
and 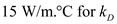 .
.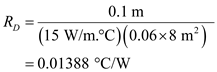 Calculate the thermal resistance in wall
Calculate the thermal resistance in wall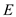 due to conduction, by using the equation as follows:
due to conduction, by using the equation as follows: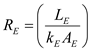 Here, the thickness of the wall
Here, the thickness of the wall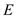 is
is 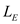 , thermal conductivity of wall
, thermal conductivity of wall 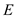 is
is 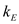 and the area normal to the direction of heat flow through
and the area normal to the direction of heat flow through  is
is 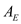 .Substitute
.Substitute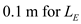 ,
, 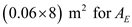 and
and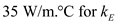 .
.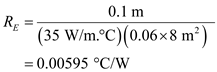
Comment Step 7 of 13
Calculate the thermal resistance in wall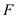 due to conduction, by using the equation as shown below.
due to conduction, by using the equation as shown below.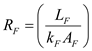 Here, the thickness of the wall
Here, the thickness of the wall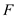 is
is 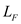 , thermal conductivity of the wall
, thermal conductivity of the wall 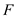 is
is 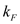 and the area normal to the direction of heat flow through
and the area normal to the direction of heat flow through 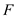 is
is 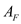 .Substitute
.Substitute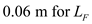 ,
,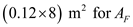 and
and 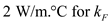 .
.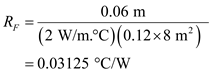
Comments (5) Step 8 of 13
The three resistances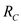 ,
,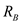 and
and 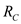 in the middle are parallel.Calculate the equivalent resistance of
in the middle are parallel.Calculate the equivalent resistance of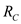 ,
, 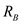 and
and 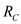 , by using the equation as shown below.
, by using the equation as shown below.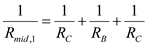 Substitute the known values in the above equation.
Substitute the known values in the above equation.
Comment Step 9 of 13
The two resistances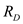 and
and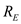 in the middle are parallel.Calculate the equivalent resistance of
in the middle are parallel.Calculate the equivalent resistance of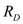 and
and 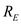 by using the equation as shown below.
by using the equation as shown below.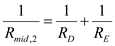 Substitute the known values in the above equation.
Substitute the known values in the above equation.
Comment Step 10 of 13
Calculate the total thermal resistance.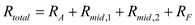 Substitute the known values in the above equation.
Substitute the known values in the above equation.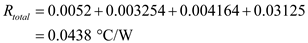
Comment Step 11 of 13
Calculate the rate of heat transfer by using the equation as shown below.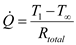 Here, the temperature of the left surface is
Here, the temperature of the left surface is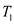 and the temperature of the right surface is
and the temperature of the right surface is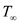 .Substitute
.Substitute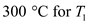 ,
,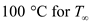 and
and 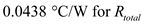 .
.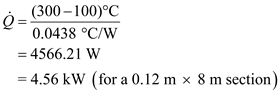 Calculate the rate of heat transfer through entire wall
Calculate the rate of heat transfer through entire wall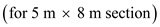 .
.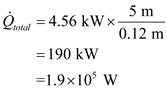 Therefore, the rate of heat transfer through the wall is
Therefore, the rate of heat transfer through the wall is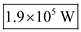 .b)Calculate the total thermal resistance between left surface and the point where the sections B, D, and E meet.
.b)Calculate the total thermal resistance between left surface and the point where the sections B, D, and E meet.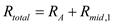 Substitute the known values in the above equation.
Substitute the known values in the above equation.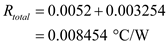
Comments (2) Step 12 of 13
Calculate the temperature at the point where the sections B, D, and E meet.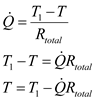 Substitute
Substitute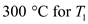 ,
, 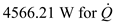 and
and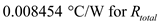 .
.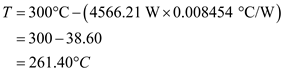 Therefore, the temperature at B, D, and E interface is
Therefore, the temperature at B, D, and E interface is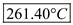 .
.Comment Step 13 of 13
c)Calculate the temperature drop across the section F by using the equation as shown below.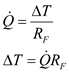 Substitute
Substitute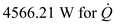 and
and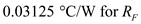 .
.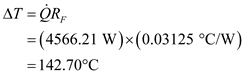 Therefore, the temperature drop across the section F is
Therefore, the temperature drop across the section F is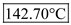 .
.Comment
