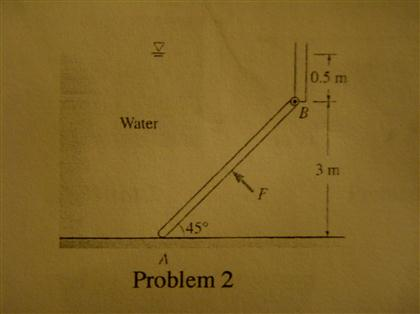
The 200-kg, 5-m wide rectangular gate is hinged at B and leans against the floor at A, making an angle of 45° with the horizontal.  The gate is to be opened from its lower edge by applying a normal force at its center.  Determine the minimum force F required to open the water gate. 

PLEASE POST SOLUTION, STEP-BY-STEP. THANKS!!!

View comments (2) 

Expert Answer

Was this answer helpful?

---

General guidance

Concepts and reason

The concepts required to solve this problem are hydrostatic forces in fluids, center of pressure, and moment.

Hydrostatic forces in fluids: When the fluid comes in contact with the surface, then the force exerted by the static fluid on the surface is termed as hydrostatic force and the direction of this force is normal to the surface.

Center of pressure: It is the point of application of the resultant pressure on the surface.

Moment: The moment is the turning effect of force and thus it is calculated by multiplying the perpendicular distance of a force from the required point and the magnitude of force.

Firstly, calculate the resultant force acting on the gate. Then locate the center of pressure. Finally, with the help of moment expression, calculate the minimum force $F$ that is required to open the water gate.

Fundamentals

The expression for hydrostatic force/resultant force acting on a submerged surface is written as:

$F = \rho g\bar xA$

Here, $\rho$ is the density of the fluid, $g$ is the acceleration due to gravity, $\bar x$ is the distance of the centroid from the free surface, and $A$ is the area of the submerged surface.

The depth of center of pressure from the liquid surface is calculated by using the formula:

$\bar h = \frac{{{I_{\rm{G}}}{{\sin }^2}\theta }}{{A\bar x}} + \bar x$

Here, $A$ and $\bar x$ are the area of immersed surface and depth of center of gravity of the immersed surface from the liquid surface, $\theta$ is the angle of inclination, and ${I_{\rm{G}}}$ is the moment of inertia of immersed surface about the horizontal axis through its center of gravity.

The expression to calculate the moment about any point $O$ due to a force applied at a given point $B$ is,

${M_O} = {r_{OB}}\left( F \right)$

Here, ${r_{OB}}$ is the perpendicular distance between O and B and $F$ is the force applied at point B.

Show less 

FIRST STEP | ALL STEPS | ANSWER ONLY

Step-by-step

Step 1 of 3

Draw the free body diagram for the gate.

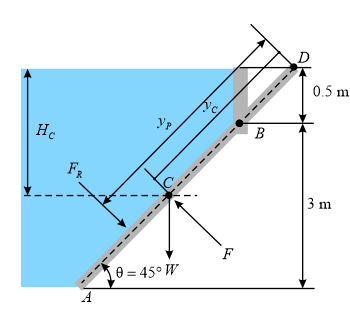
In the above free body diagram, ${F_R}$ is the hydrostatic force on the gate due to the fluid lying above, C is the centroid of the gate, $D$ is a point such that it is along the inclination of gate and lies at the free surface, ${H_C}$ is the distance of the centroid of the gate from the free surface, ${y_C}$ is the distance of the centroid of the gate along the inclination of gate, $\theta$ is the angle of inclination of gate AB with the horizontal, ${y_P}$ is the position of center of pressure, and $W$ is the weight of the gate.

Consider the length of the gate AB from principles of trigonometry.

$\frac{{3{\rm{ m}}}}{l} = \sin 45^\circ$

Rearrange l.

$\begin{array}{c}\\l = \frac{{3{\rm{ m}}}}{{\sin 45^\circ }}\\\\ = 4.24{\rm{ m}}\\\end{array}$

Calculate the length BC.

$BC = \frac{l}{2}$

Substitute $4.24{\rm{ m}}$ for $l$ .

$\begin{array}{c}\\BC = \frac{{4.24{\rm{ m}}}}{2}\\\\ = 2.12{\rm{ m}}\\\end{array}$

Calculate the distance between the free surface and the centroid of the gate.

${H_C} = 0.5{\rm{ m}} + BC\sin 45^\circ$

Substitute $2.12{\rm{ m}}$ for BC.

$\begin{array}{c}\\{H_C} = 0.5{\rm{ m}} + \left( {2.12{\rm{ m}}} \right)\sin 45^\circ \\\\ = 0.5{\rm{ m}} + \left( {2.12{\rm{ m}}} \right)\left( {\frac{1}{{\sqrt 2 }}} \right)\\\\ = 2{\rm{ m}}\\\end{array}$

Calculate the area of the gate.

${A_g} = wl$

Here, w is the width of the gate.

Substitute $5{\rm{ m}}$ for $w$ and $4.24{\rm{ m}}$ for $l$ .

$\begin{array}{c}\\{A_g} = \left( {5{\rm{ m}}} \right)\left( {4.24{\rm{ m}}} \right)\\\\ = 21.2{\rm{ }}{{\rm{m}}^2}\\\end{array}$

Write the expression for hydrostatic force on the gate.

${F_R} = \rho g{H_C}{A_g}$

Substitute $1000{\rm{ kg/}}{{\rm{m}}^3}$ for $\rho$ , $9.81{\rm{ m/}}{{\rm{s}}^2}$ for $g$ , $2{\rm{ m}}$ for ${H_C}$ , and $21.2{\rm{ }}{{\rm{m}}^2}$ for ${A_g}$ .

$\begin{array}{c}\\{F_R} = \left( {1000{\rm{ kg/}}{{\rm{m}}^3}} \right)\left( {9.81{\rm{ m/}}{{\rm{s}}^2}} \right)\left( {2{\rm{ m}}} \right)\left( {21.2{\rm{ }}{{\rm{m}}^2}} \right)\\\\ = 415944{\rm{ N}}\\\end{array}$

Explanation | Common mistakes | Hint for next step

The water above the gate creates a force on the gate which acts at the center of pressure. The dimensions that are provided are used to calculate the distance of the centroid of the gate from the free surface. Basic principle of trigonometry, such as $\sin \theta = \frac{{{\rm{perpendicular}}}}{{{\rm{Hypotenuse}}}}$ for a right angled triangle, is used for this purpose.

The value of distance of the centroid of the gate from the free surface is used to evaluate the hydrostatic/resultant force on the gate. The direction of this force is normal to the surface of the gate.

Step 2 of 3

Calculate the moment of inertia of the gate about the $x$ axis.

${I_{xx}} = \frac{{w{l^3}}}{{12}}$

Substitute $5{\rm{ m}}$ for $w$ and $4.24{\rm{ m}}$ for $l$ .

$\begin{array}{c}\\{I_{xx}} = \frac{{\left( {5{\rm{ m}}} \right){{\left( {4.24{\rm{ m}}} \right)}^3}}}{{12}}\\\\ = 31.76{\rm{ }}{{\rm{m}}^4}\\\end{array}$

Write the expression for depth of center of pressure from the free surface.

$\bar h = \frac{{{I_{\rm{G}}}{{\sin }^2}\theta }}{{{A_g}{H_C}}} + {H_C}$

Substitute $31.76{\rm{ }}{{\rm{m}}^4}$ for ${I_{xx}}$ , $45^\circ$ for $\theta$ , $2{\rm{ m}}$ for ${H_C}$ , and $21.2{\rm{ }}{{\rm{m}}^2}$ for ${A_g}$ .

$\begin{array}{c}\\\bar h = \frac{{\left( {31.76{\rm{ }}{{\rm{m}}^4}} \right){{\sin }^2}45^\circ }}{{\left( {21.2{\rm{ }}{{\rm{m}}^2}} \right)\left( {2{\rm{ m}}} \right)}} + 2{\rm{ m}}\\\\ = 2.3745{\rm{ m}}\\\end{array}$

Calculate the distance of the pressure center from the point D from the concept of trigonometry.

${y_P} = \frac{{\bar h}}{{\sin \theta }}$

Substitute $2.3745{\rm{ m}}$ for $\bar h$ and $45^\circ$ for $\theta$ .

$\begin{array}{c}\\{y_P} = \frac{{\left( {2.3745{\rm{ m}}} \right)}}{{\sin 45^\circ }}\\\\ = 3.358{\rm{ m}}\\\end{array}$

Explanation | Common mistakes | Hint for next step

The moment of inertia of the gate is evaluated about its centroid axis by using the expression for a rectangular area. The expression for distance of center of pressure from the free surface is written. The values of the known parameters are substituted ion the expression to calculate its value.

The distance of the pressure center from the point D is calculated from the concept of trigonometry. Basic principle of trigonometry, such as $\sin \theta = \frac{{{\rm{perpendicular}}}}{{{\rm{Hypotenuse}}}}$ for a right angled triangle, is used for this purpose.

Step 3 of 3

Calculate the moment about B applied by the weight of the gate and the resultant hydrostatic force on the gate.

${M_{B,g}} = {F_R}\left( {{y_p} - \frac{{0.5{\rm{ m}}}}{{\sin 45^\circ }}} \right) + W\left( {\frac{l}{2}\cos 45^\circ } \right)$

Calculate the moment about B due to the applied force F.

${M_{B,Fg}} = F\left( {\frac{l}{2}} \right)$

Consider the requirement of the question and understand that to lift the gate the moment applied by force F must be equal to that B applied by the weight of the gate and the resultant hydrostatic force on the gate.

${M_{B,Fg}} = {M_{B,g}}$

Substitute $F\left( {\frac{l}{2}} \right)$ for ${M_{B,Fg}}$ and ${F_R}\left( {{y_p} - \frac{{0.5{\rm{ m}}}}{{\sin 45^\circ }}} \right) + W\left( {\frac{l}{2}\cos 45^\circ } \right)$ for ${M_{B,g}}$ .

$F\left( {\frac{l}{2}} \right) = {F_R}\left( {{y_p} - \frac{{0.5{\rm{ m}}}}{{\sin 45^\circ }}} \right) + W\left( {\frac{l}{2}\cos 45^\circ } \right)$

Substitute $415944{\rm{ N}}$ for ${F_R}$ , $3.358{\rm{ m}}$ for ${y_p}$ , $200{\rm{ kg}}$ for $m$ , $9.81{\rm{ m/}}{{\rm{s}}^2}$ for $g$ , and $4.24{\rm{ m}}$ for $l$ .

$\begin{array}{l}\\F\left( {\frac{{4.24{\rm{ m}}}}{2}} \right) = \left( {415944{\rm{ N}}} \right)\left( {3.358{\rm{ m}} - \frac{{0.5{\rm{ m}}}}{{\sin 45^\circ }}} \right) + \left( {200{\rm{ kg}}} \right)\left( {9.81{\rm{ m/}}{{\rm{s}}^2}} \right)\left( {\frac{{4.24{\rm{ m}}}}{2}\cos 45^\circ } \right)\\\\{\rm{2}}{\rm{.12 m}}\left( F \right) = \left( {415944{\rm{ N}}} \right)\left( {3.356{\rm{ m}} - 0.707{\rm{ m}}} \right) + \left( {200{\rm{ kg}}} \right)\left( {9.81{\rm{ m/}}{{\rm{s}}^2}} \right)\left( {1.499{\rm{ m}}} \right)\\\\F = \frac{{\left( {415944{\rm{ N}}} \right)\left( {2.651{\rm{ m}}} \right) + \left( {200{\rm{ kg}}} \right)\left( {9.81{\rm{ m/}}{{\rm{s}}^2}} \right)\left( {1.499{\rm{ m}}} \right)}}{{{\rm{2}}{\rm{.12 m}}}}\\\\F = 521500{\rm{ N}}\\\end{array}$

Further solve as,

$F = 521.5{\rm{ kN}}$

The minimum force required to open the water gate is $521.5{\rm{ kN}}$ .

Explanation | Common mistakes

The moment about point B is due to the weight and the hydrostatic force on the gate. In order to open the gate, the force applied must be able to overcome this net moment. So, this concept is used and the moment due to the respective quantities are equated. The values of known parameters are substituted in the equation to evaluate the value of force required.

Answer

The minimum force required to open the water gate is $521.5{\rm{ kN}}$ .