Problem
An automatic welding machine is being considered for use in a production process. It will be considered for purchase if it is successful on 99% of its welds. Otherwise, it will not be considered efficient. A test is to be conducted with a prototype that is to perform 100 welds. The machine will be accepted for manufacture if it misses no more than 3 welds.
(a) What is the probability that a good machine will be rejected?
(b) What is the probability that an inefficient machine with 95% welding success will be accepted?
Step-by-step solution
Step 1 of 4
(a)The automatic welding machine will be purchased if it misses no more than 3 welds out of 100 welds in the prototype. The success rate of the welding machine is 99%. Let X denotes the number of missed welds in the 100 welds performed by the welding machine. Then X follows binomial distribution with parameter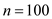
and 
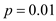.The probability distribution of X is denoted by the function below.
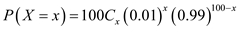for x = 0, 1, 2 ... 100.Comment Step 2 of 4
The probability that a good machine will be rejected is the probability that the number of missed welds is greater than 3 welds in the 100 welds. It is denoted by the probability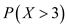
.
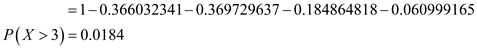The probability that a good machine will be rejected is 0.0184.Comment Step 3 of 4
(b)The probability distribution of number of missed welds in 100 welds of the inefficient machine with 95% welding success is given below.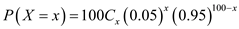
for x = 0, 1, 2 ... 100.Comment Step 4 of 4
The probability that this inefficient machine will be accepted is the probability that the number of welds is at most 3 missed welds in the 100 welds. It is denoted by the probability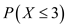
.
The probability that inefficient machine with 95% success will be accepted is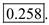
Comment
