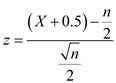- ahmad alhayek

Problem

Perform these steps.

a. Slate the hypotheses and identify the claim.
b. Find the critical value(s).
c. Compute the test value.
d. Make the decision.
e. Summarize the results.

Use the traditional method of hypothesis testing unless otherwise specified.

Exam Scores A statistics professor wants to investigate the relationship between a student’s midterm examination score and the score on the final. Eight students were randomly selected, and their scores on the two examinations are noted. At the 0.10 level of significance, is there sufficient evidence to conclude that there is a difference in scores?

Step-by-step solution

Step 1 of 13
a.
Comment
Step 2 of 13
State the hypotheses.
Comment
Step 3 of 13
Null hypothesis:
There is no difference in the exam scores.
Alternative hypothesis:
There is a difference in the exam scores (Claim).
Comment
Step 4 of 13
b.
Comment
Step 5 of 13
Compute the critical value.
Comment
Step 6 of 13
Since the sample size (n) is 8, there are 8 degrees of freedom and the alternative hypothesis is denoted as the two tailed test. If the sample size is less than 25, then the small-sample test statistic is obtained. Hence, the critical values obtained from Table J at 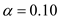and 8 degrees of freedom is 1.
Hence, the critical value is .
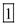Comment
Step 7 of 13
c.
Comment
Step 8 of 13
Find the test value.
Comment
Step 9 of 13
The difference 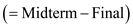of each individual data to obtain the sign is calculated below:
Comment
Step 10 of 13
Difference
Signs
–7
–
2
+
–11
–
–10
–
–5
–
–3
–
3
+
1
+
Therefore, the table represents that there are 3 pluses and 5 minuses. The alternative hypothesis is denoted as the two tailed test. The general term for test statistic is as follows:
Type of test
Test statistic
Right–tailed test
Number of Minus signs.
Left–tailed test
Number of Plus signs.
Two–tailed test
Number of Plus or Minus signs, whichever is smaller.
Hence the test value is .
Comment
Step 11 of 13
d.
Comment
Step 12 of 13
Make the decision.
From the results obtained in part (b) and part (c), it is clear that the test value is 3 and the critical value is 1.
Here, the test value is greater than the critical value. That is, .
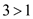Therefore, by the rejection rule, do not reject the null hypothesis .
Comment
Step 13 of 13
e.
Summarize the result.
There is no sufficient evidence to conclude that there is a difference in the exam scores at .
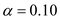Comment

Problem

Perform these steps.

a. Slate the hypotheses and identify the claim.
b. Find the critical value(s).
c. Compute the test value.
d. Make the decision.
e. Summarize the results.

Use the traditional method of hypothesis testing unless otherwise specified.

Number of Faculty for Proprietary Schools An educational researcher believes that the median number of faculty for proprietary (for-profit) colleges and universities is 150. The data provided list the number of faculty at a randomly selected number of proprietary colleges and universities. At the 0.05 level of significance, is there sufficient evidence to reject his claim?

Step-by-step solution

Step 1 of 16
a.
Comment
Step 2 of 16
State the hypotheses.
Comment
Step 3 of 16
Null hypothesis:
The population median is same as 150 (Claim).
That is, .
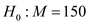Alternative hypothesis:
The population median is not same as 150.
That is, .
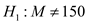Comment
Step 4 of 16
b.
Comment
Step 5 of 16
Compute the critical value.
Comment
Step 6 of 16
Since the sample size (n) is 35, there are 35 degrees of freedom and the alternative hypothesis is denoted as the two tailed test. Hence, the critical values obtained from Table E at 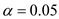and 35 degrees of freedom is .
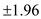Hence, the critical value is .
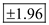Comment
Step 7 of 16
c.
Comment
Step 8 of 16
Find the test value.
Comment
Step 9 of 16
The formula for test value is as follows:
Comment
Step 10 of 16
Comment
Step 11 of 16
Where X is the number of signs whichever is smaller and n is the total number of sample sizes.
Comment
Step 12 of 16
Use MINITAB to analyze the given data.
MINITAB procedure:
Step 1: Choose Stat > Nonparametrics > 1-Sample Sign.
Step 2: In Variables, enter the column of Faculty.
Step 3: Choose the Test median, enter the value as 150 and select the appropriate Alternative.
Step 4: Click OK.
Comment
Step 13 of 16
MINITAB output:
Hence the value for X is .
Comment
Step 14 of 16
Therefore, the test value is calculated as follows:
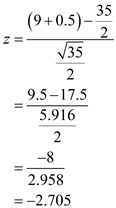
Hence the test value is .
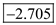Comment
Step 15 of 16
d.
Make the decision.
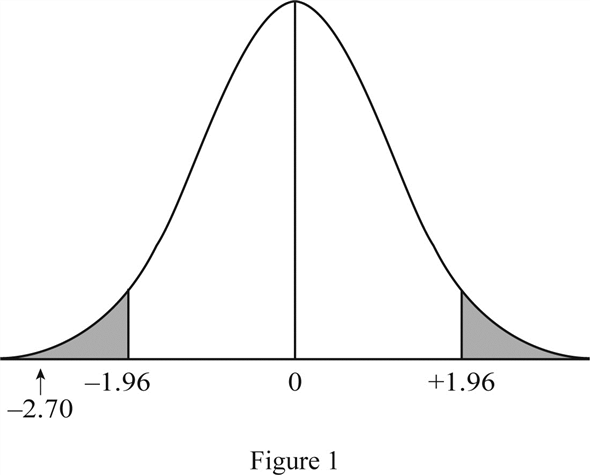
From the results obtained in part (b) and part (c), it is clear that the test value is –2.705 and the critical value is –1.96.
Sketch the critical region.
The critical region of two-tailed is shown in Figure (1).
$Z:\CHEGG\01_Solutions_Authoring\Statistics\202674\04_Artwork\202674-13.2-11E.jpg$
Here, the test value is lesser than the critical value. That is, .
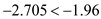Therefore, by the rejection rule, reject the null hypothesis .
Comment
Step 16 of 16
e.
Summarize the results.
There is sufficient evidence to conclude that the population median is not same as 150 at .
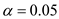Comment
Problem
Perform these steps.
a. Slate the hypotheses and identify the claim.
b. Find the critical value(s).
c. Compute the test value.
d. Make the decision.
e. Summarize the results.
Use the traditional method of hypothesis testing unless otherwise specified.
Diet Medication and Weight A study was conducted to see whether a certain diet medication had an effect on the weights (in pounds) of eight randomly selected women. Their weights were taken before and six weeks after daily administration of the medication. The data are shown here. At α = 0.05, can you conclude that the medication had an effect (increase or decrease) on the weights of the women?
Step-by-step solution
1. Step 1 of 13
  a.
  Comment
2. Step 2 of 13
  State the hypotheses.
  Comment
3. Step 3 of 13
  Null hypothesis:
  The medication has no effect on the weight loss.
  Alternative hypothesis:
  The medication has an effect on the weight loss (Claim)
  Comment
4. Step 4 of 13
  b.
  Comment
5. Step 5 of 13
  Compute the critical value.
  Comment
6. Step 6 of 13
  Since the sample size (n) is 8, there are 8 degrees of freedom and the alternative hypothesis is denoted as the two tailed test. If the sample size is less than 25, then the small-sample test statistic is obtained. Hence, the critical values obtained from Table J at 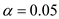and 8 degrees of freedom is 0.
  Hence, the critical value is .
  Comment
7. Step 7 of 13
  c.
  Comment
8. Step 8 of 13
  Find the test value.
  Comment
9. Step 9 of 13
  The difference 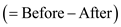of each individual data to obtain the sign is calculated below:
  Comment
10. Step 10 of 13
  Difference
  Signs
  9
  +
  1
  +
  13
  +
  2
  +
  6
  +
  –7
  –
  23
  +
  4
  +
  Therefore, the table represents that there are 7 pluses and 1 minus. The alternative hypothesis is denoted as the two tailed test. The general term for test statistic is as follows:
  Type of test
  Test statistic
  Right-tailed test
  Number of Minus signs.
  Left-tailed test
  Number of Plus signs.
  Two-tailed test
  Number of Plus or Minus signs, whichever is smaller.
  Hence the test value is .
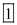  Comment
11. Step 11 of 13
  d.
  Comment
12. Step 12 of 13
  Make the decision.
  From the results obtained in part (b) and part (c), it is clear that the test value is 1 and the critical value is 0.
  Here, the test value is greater than the critical value. That is, .
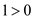  Therefore, by the rejection rule, do not reject the null hypothesis .
  Comment
13. Step 13 of 13
  e.
  Summarize the result.
  There is no sufficient evidence to conclude that the medication has an effect on the weight loss of the women at .
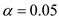  Comment

Difference	Signs
–7	–
2	+
–11	–
–10	–
–5	–
–3	–
3	+
1	+

Type of test	Test statistic
Right–tailed test	Number of Minus signs.
Left–tailed test	Number of Plus signs.
Two–tailed test	Number of Plus or Minus signs, whichever is smaller.

Type of test	Test statistic
Right-tailed test	Number of Minus signs.
Left-tailed test	Number of Plus signs.
Two-tailed test	Number of Plus or Minus signs, whichever is smaller.

ahmad alhayek

Step 1 of 13

Step 2 of 13

Step 3 of 13

Step 4 of 13

Step 5 of 13

Step 6 of 13

Step 7 of 13

Step 8 of 13

Step 9 of 13

Step 10 of 13

Step 11 of 13

Step 12 of 13

Step 13 of 13

Step 1 of 16

Step 2 of 16

Step 3 of 16

Step 4 of 16

Step 5 of 16

Step 6 of 16

Step 7 of 16

Step 8 of 16

Step 9 of 16

Step 10 of 16

Step 11 of 16

Step 12 of 16

Step 13 of 16

Step 14 of 16

Step 15 of 16

Step 16 of 16