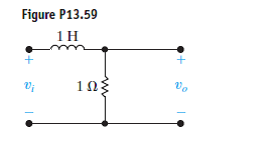
Problem

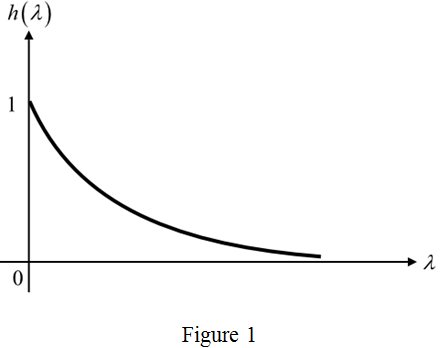
A rectangular voltage pulse v_i = [u(t) - u(t - 1)] V is applied to the circuit in Fig. P13.59. Use the convolution integral to find v_o.

Step-by-step solution

1. Step 1 of 8

   Refer to Figure P13.59 in the textbook for the circuit diagram.

   The s-domain representation of the circuit is shown in Figure 1.

   

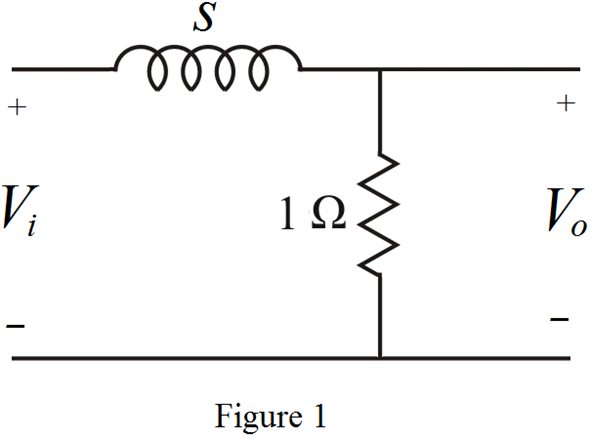
   Comment

2. Step 2 of 8

   Calculate the output voltage using voltage division rule.

   

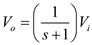
   The transfer function is,

   

   Apply inverse Laplace transform on both sides.

   

   Replace  with .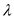

   

   Here, the impulse response is a decaying exponential. So, plot the impulse function.

   

   Comment

3. Step 3 of 8

   Consider the input voltage, . Replace  with .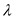

   

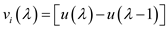
   The mathematical representation is,

   

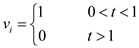
   Plot the input signal.

   

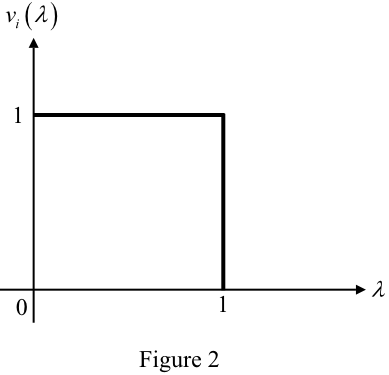
   Comment

4. Step 4 of 8

   The folded excitation function  is shown in Figure 3.

   

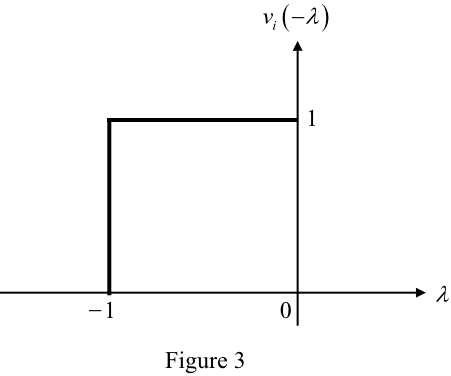
   The convolution integral is,

   

   Plot the signal, .

   

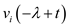   Comment

5. Step 5 of 8

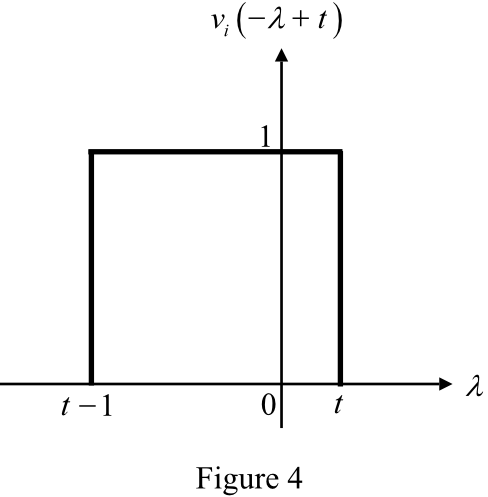
   Apply the convolution to both Figure 4 and Figure 1.

   

   Comment

6. Step 6 of 8

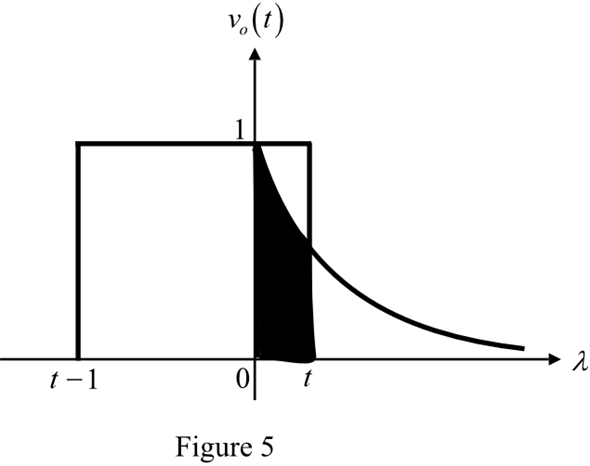
   From Figure 5, the output voltage in the interval of 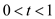 is,

   

   Comment

7. Step 7 of 8

   Now apply the convolution to both Figure 4 (when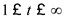) and Figure 1.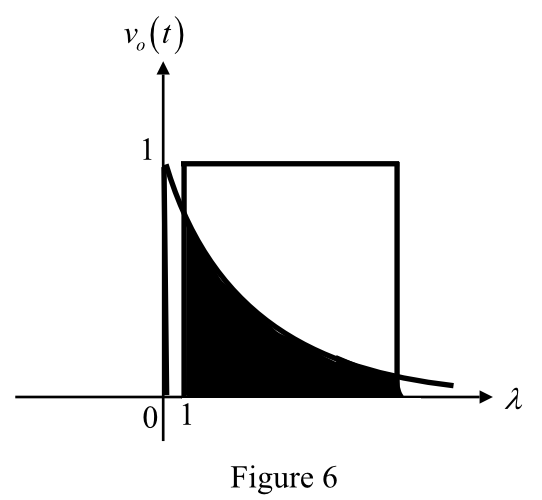

   

   Comment

8. Step 8 of 8

   From Figure 5, the output voltage in the interval of 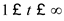 is,

   

   The output waveform is shown in Figure 7.

   

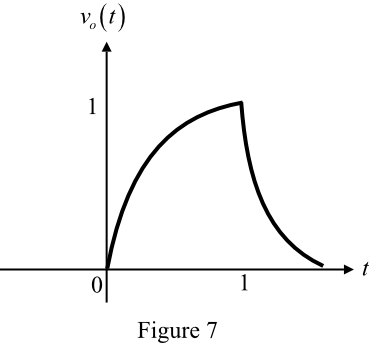
   Hence, the output has been obtained.

   Comments (1)