Problem
Oil flow in a Journal bearing can be treated as parallel flow between two large isothermal plates with one plate moving at a constant velocity of 8 m/s and the other stationary. Consider such a flow with a uniform spacing of 0.7 mm between the plates. The temperatures of the upper and lower plates are 40°C and 15°C, respectively. By simplifying and solving the continuity, momentum, and energy equations, determine (a) the velocity and temperature distributions in the oil, and (b) the maximum temperature and where it occurs, and (c) the heat flux from the oil to each plate.
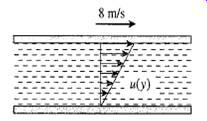
FIGURE P6-49.
Step-by-step solution
Step 1 of 10
2134-6-49P AID: 604
RID: 241
Comments (1) Step 2 of 10
Given
Constant velocity of moving plate
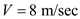
Spacing between the two plates
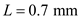
Temperature of upper plate
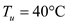
Temperature of lower plate
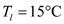
Given that oil flow in a journal bearing can be treated as parallel flow between two large isothermal plates with one plate moving at constant velocity and other plate as stationary
Comment Step 3 of 10
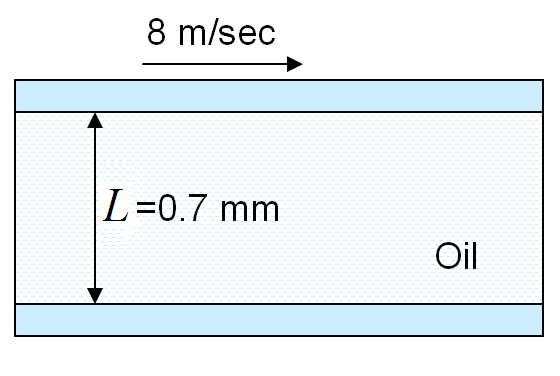
The average temperature of oil is
From properties of liquids Properties of engine oil at average temperature
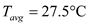
Thermal conductivity
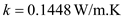
Dynamic viscosity
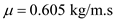
Consider the flow direction is along x-axis and the y-axis to be the normal direction
Let the velocity in the flow and normal directions as
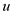and 
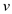respectivelyGiven the parallel flow between the plates, hence the velocity in the normal direction is equal to zero i.e.,
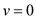
Applying the continuity equation
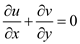
As
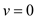, the continuity equation reduces to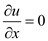
Hence
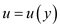this means that the x-component of velocity changes with normal direction and does not change in flow direction.Comment Step 4 of 10
Given that the upper plate is moving with constant velocity, which means that the flow is maintained by the motion of the upper plate rather than pressure gradient, so
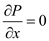
Applying the x-momentum equation,
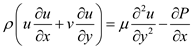
Since
,
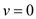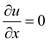and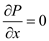
The momentum equation reduces to
Integrating twice the second-order differential equation gives
Where
and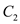 
are constantsComment Step 5 of 10
The fluid velocities at the plate surfaces must be equal to the velocities of the plates because of the no-slip condition.
Therefore, from the given data, the known boundary conditions are
At
, 
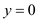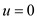andAt
, 
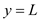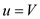
Applying these two conditions in the expression
,Applying first boundary condition
,
Then applying second boundary condition
in the differential equation
Comment Step 6 of 10
Then substituting the two constant values in the differential equation
Comment Step 7 of 10
From the energy equation,
Given the plates are isothermal and there is no change in the flow direction, and thus the temperature depends on y only then we have
As
,
, 
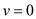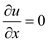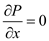and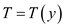 
the energy equation reduces to 
From the above velocity distribution
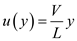
Differentiating the above equation
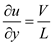
Hence the energy equation becomes
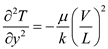
Integrating twice the above second-order differential equation gives
Where
and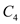 
are constantsComment Step 8 of 10
The fluid temperatures at the plate surfaces must be equal to the temperatures of the plates because of the no-temperature slip condition
Therefore, from the given data, the known boundary conditions are
At
, 
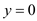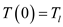andAt
, 
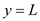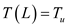
Applying first boundary condition in the expression
,At
,
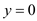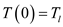
Applying second boundary condition
At
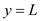
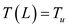
Finally, the temperature distribution gives as
Therefore the velocity and temperature distributions in the oil are
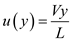and 
(b)
We know the temperature distribution in the oil is
The temperature gradient is determined by differentiating
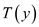with respect to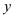 
The location of maximum temperature is determined by setting
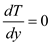and solving for
,
Substituting the values in the above expression
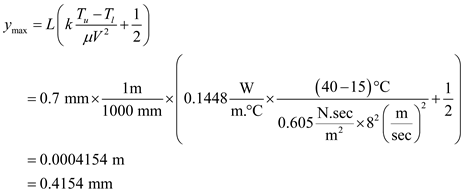
Then the maximum temperature is obtained at substituting
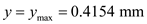in the temperature distribution equation
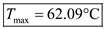
Therefore the maximum temperature occur in the oil is
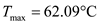
Comment Step 9 of 10
(c) Heat flux at the plates is determined from the definition of heat flux,
At lower plate,
Comment Step 10 of 10
At upper plate,
Comment
