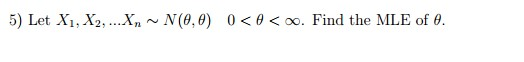
Expert Answer
 Comment
CommentSince
. Define the likelihood function as
Differentiate with respect to
gives
Now
gives
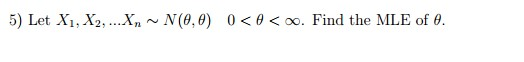
Since . Define the likelihood function as
Differentiate with respect to gives
Now gives
ahmad alhayek تصميم ahmad alhayek جميع الحقوق محفوظة 2016
ليست هناك تعليقات:
إرسال تعليق